Neural Correlates of Control of a Kinematically Redundant Brain-Machine Interface
Introduction
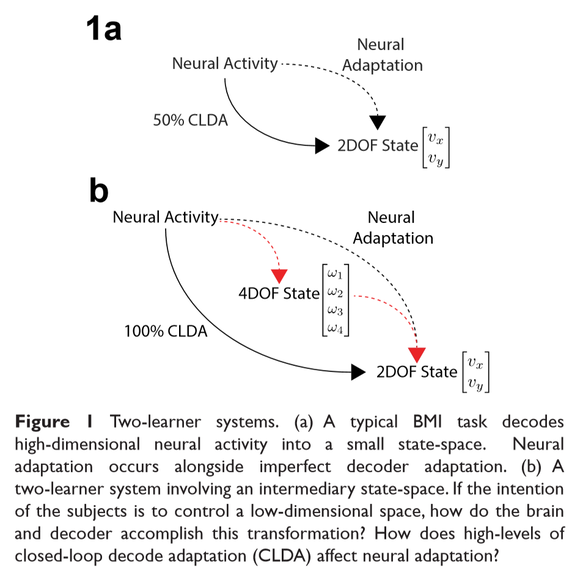
Brain-machine interfaces (BMI) allow users to interact with their environments by decoding neural intentions into commands that move an effector. Past studies have shown that neurons adapt to decoders over learning. Furthermore, current decoder algorithms allow for high performance in early training. However, it is unclear how neurons may adapt in this “two-learner” system if the decoder accurately represents neural intentions (Figure 1). Additionally, will neurons adapt if decoder weights are refit daily? Finally, while the majority of BMI experiments have utilized low-dimensional effectors, little is known about how a two-learner system resolves control of a kinematically-redundant BMI.
Methods
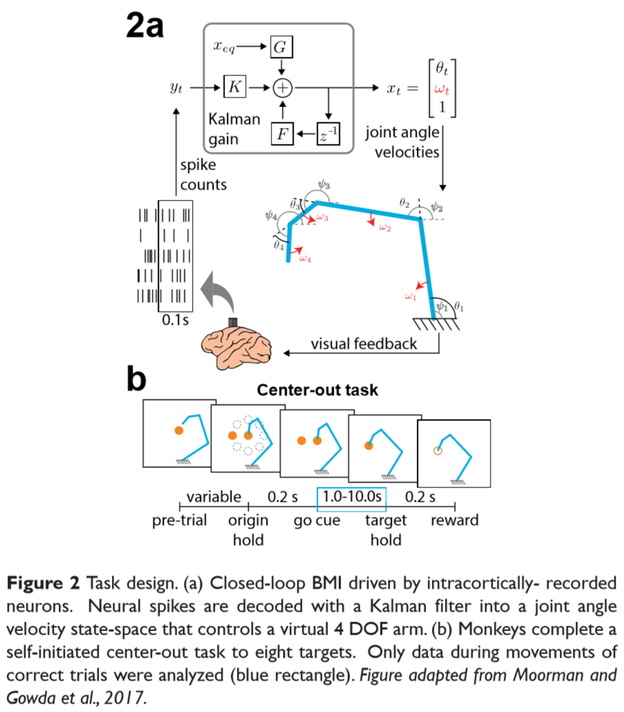
Data was previously collected by Moorman and Gowda et al., 2017. Chronic microelectrode arrays were implanted bilaterally into two rhesus macaques. Spikes were recorded and binned in 100 ms time windows and used to drive a Kalman filter decoder seeded on visual feedback. Neural activity was decoded into 4 joint angle velocities to move a cursor in 2D space, thereby generating the kinematic redundancy. Decoders were refit at the start of each session and both animals were previously trained a simpler BMI task (2D cursor to 2D targets).
Results
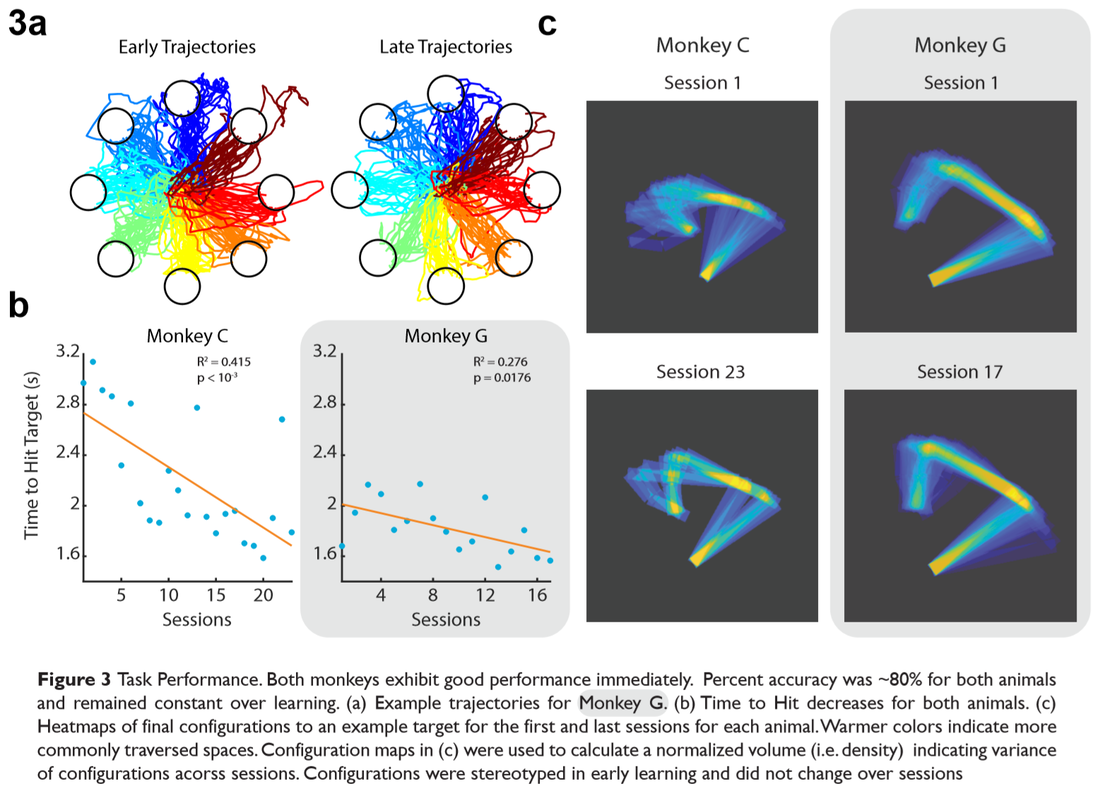
To observe behavioral changes over learning, we first looked at reach times for each animal across days (Figure 3 a, b). We found that reach times decreased as animals improved their control of the effector. Figure 3a shows the raw trajectories of multiple trials for an animal in early learning and late learning. We subjectively notice that the traces are more direct in late learning, indicating some form of stereotopy. To quantify this, we find the final configurations of the virtual arm for each trial and overlay them on top of each other to get a distribution of where the final configurations are (Figure 3c). We find that for both animals, the virtual arms form more stereotyped configurations in late learning.
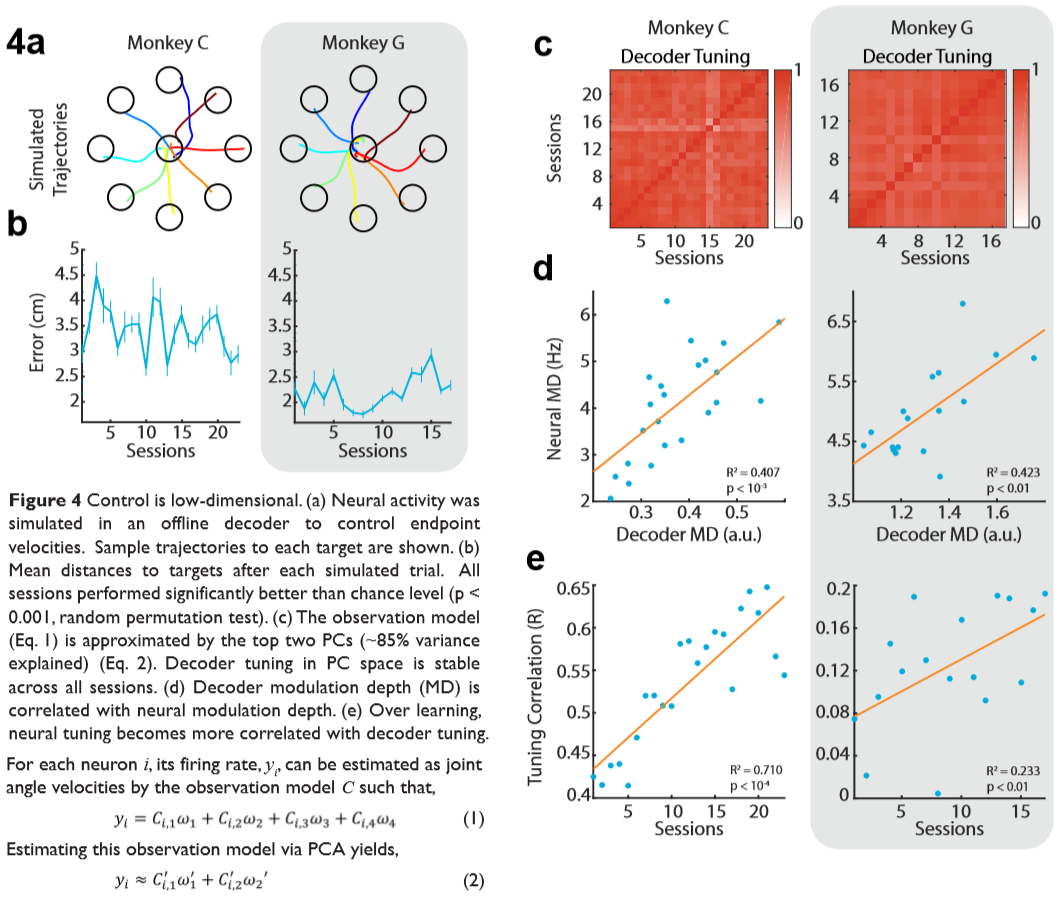
We then hypothesized that the animals did not really understand that each of the joints angles were controlled separately. Much like you and me, we don't typically move our arms by thinking explicitly about each of our joints. To test this hypothesis, we used a Kalman filter to do offline decoding on the neural activity, this time transforming spikes into cursor velocities rather than joint angle velocities. We found that in both animals, the trajectories were fairly smooth and the error to the targets was relatively low given that it was offline decoding (and therefore with no visual feedback) (Figure 4 a, b).
Furthermore, we calculated the tuning profiles of the decoder and the neurons. Neurons in motor cortex tend to have preferred tuning directions where movements in certain directions cause individual neurons to fire more aggressively. Typically, we expect decoders to be able to pick up this variance. However, since the decoder aimed to decode joint angle velocities, and the system was kinematically redundant, this estimation is not so straightforward. Thus, to approximate how the decoders estimated the neural intentions, we first use principal component analysis (PCA) to find the variance of decoder weights on two dimensions. That is, given the observation model C in a Kalman filter, a statespace \(\omega\), and neural activity y for a single neuron \(i\),
\[y_i = C_{i,1} (\omega_1) + C_{i,2} (\omega_2) + C_{i,3} (\omega_3) + C_{i,4} (\omega_4)\]
Our PCA model yields,
\[y_i = C'_{i,1} \omega'_1 + C'_{i,2} \omega'_2\]
This is loosely in the same form as a more typical Cartesian decoding schema:
\[y_i = C_{i,1} v_x + C_{i,2} v_y\]
where the tuning directions would be \(PD_i = \arctan(\frac{C_{i,2}}{C_{i,1}})\).
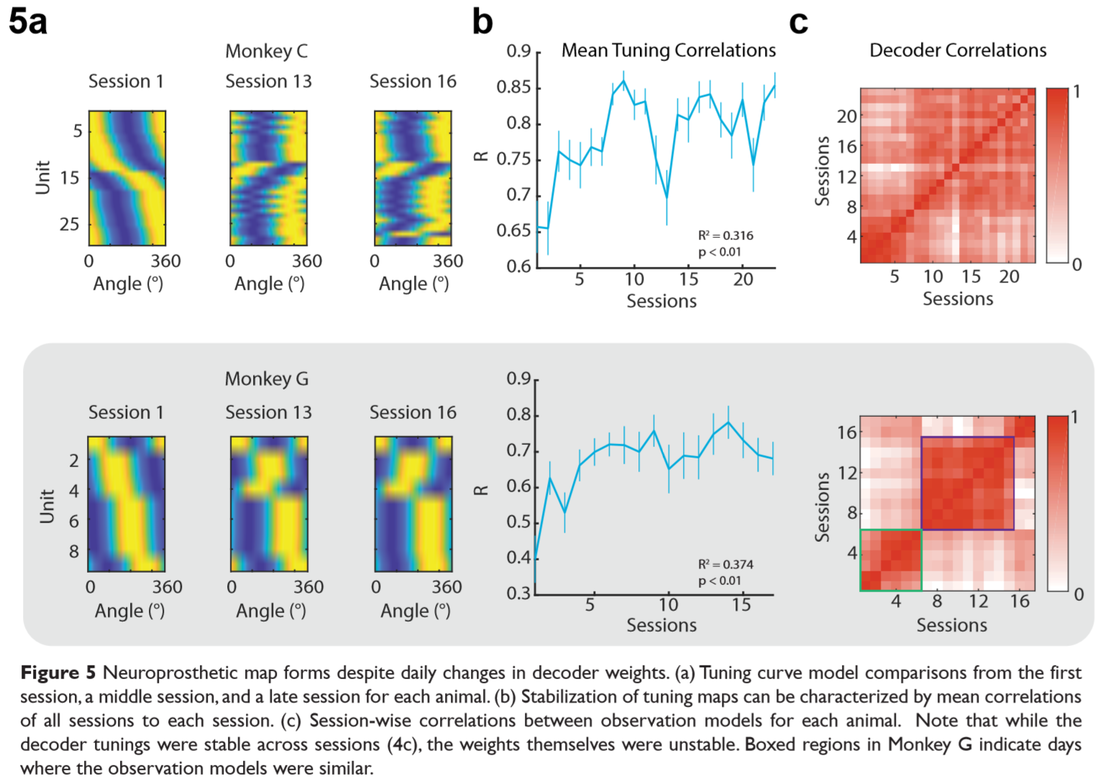
Surprisingly, we find that the decoder retains the same preferred tuning approximations for each neuron across all days (Figure 4c) and is highly correlated with the preferred directions and modulation depths of the neurons (Figure 4 d,e). Note that the modulation depths (MD) are simply the ranges in each of the tuning curves (i.e. max-min).
Despite readapting the decoder at the start of each day, the stability of the decoder tuning profiles suggests that we can approximate the decoders as being static throughout the time-series. As such, we would expect neurons to consolidate over learning, similar to results shown in previous studies such as Ganguly and Carmena, 2009 and Athalye et al., 2017.
Indeed, we find that changes in preferred tuning directions for neurons are more drastic in early learning then stabilize in late learning (Figure 5 a,b). However, notably, the decoder weights themselves were not stable. Rather, the tuning profiles generated by the decoder weights remained constant, but the raw values were not (Figure 5c).
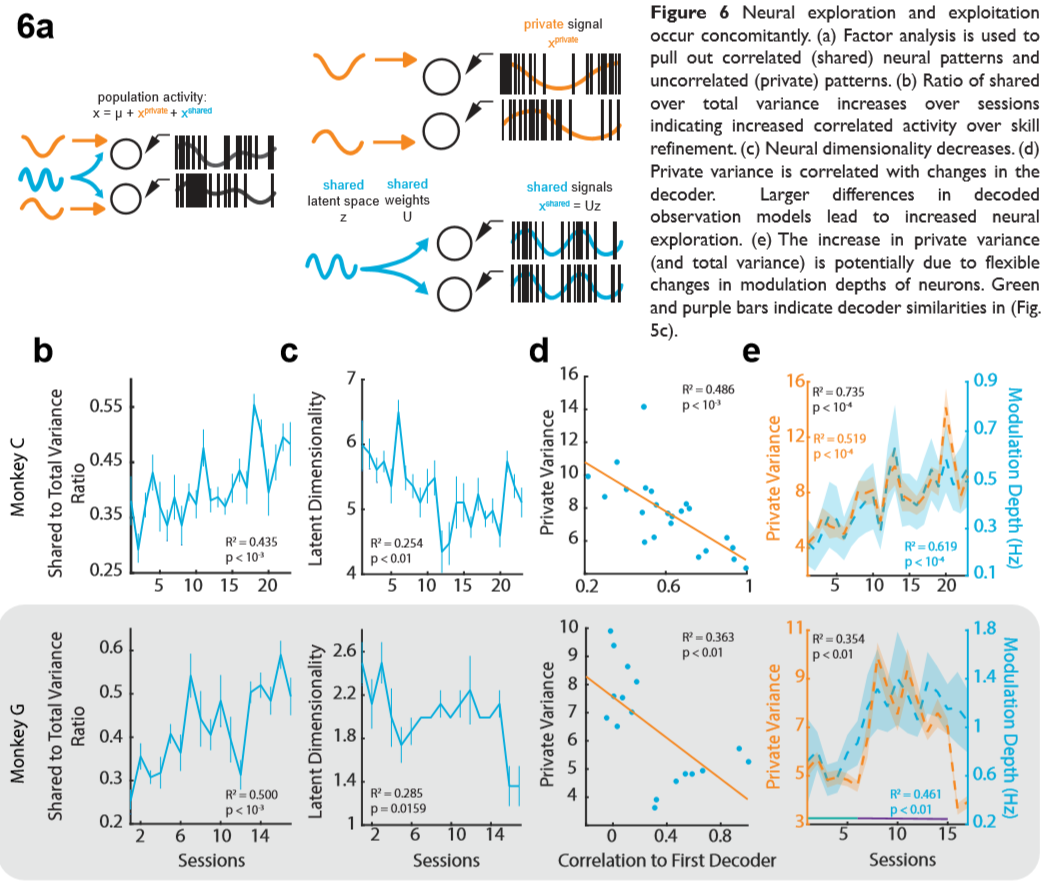
Finally, to characterize how the neurons were consolidating on a population level, we used factor analysis (FA) to find correlations of neural activity on low-dimensional subspaces (Figure 6a). Similar to findings with kinematically-deterministic effectors, we report that the correlated variance (shared) increased relative to the total variance (Figure 6b) while dimensionality decreases (Figure 6c). We also find that the private variance (i.e. variance unique to each neuron) decreased with decoders that were more similar to the first decoder the animals used and furthermore, fluctuations in private variance were correlated with changes in MD (Figure 6 d,e).
Discussion
Our results indicate that while the explicit state-space for control was kinematically redundant, it is likely animals sought only to control the endpoint of the effector rather than individual joint angles. However, this conversion from polar coordinates to Cartesian coordinates was not possible with our decoder architecture, implying that the linearization was performed by the brain. Furthermore, despite daily readaptation of the decoder, neurons were able to consolidate over time, generating stable neuroprosthetic tuning maps as performance improved.